Diffusion Model（扩散模型）是目前图像、视频生成模型的基础，其核心思想是通过逐步添加噪声（正向扩散）和逐步去噪（反向生成）的过程，将数据从原始分布逐步转换为噪声分布，再通过学习逆过程逐步去除噪音生成高质量样本。
Denoising Diffusion Probabilistic Model
Diffusion model早在2015年论文1 2
Denoising
所谓“噪音”指的是标准正态分布。
正向扩散过程：把复杂数据“拆解”成简单的噪声
正向过程的核心任务是逐步向数据中添加噪声，直到它变成完全随机的高斯噪声。这一步看似简单，但它的意义非常深刻。真实世界的数据分布往往是高度复杂的，比如图像、语音、文本，它们的特征空间可能有无数个维度，分布形态也极其不规则。直接建模这样的分布几乎是不可能。但通过正向过程，我们可以把这种复杂性“分解”掉。每一步只添加一点点噪声，逐步掩盖数据的细节，最终让数据完全服从高斯分布，这样一来，原本复杂的分布就被转化成一个简单的高斯分布，学习任务的难度大大降低。这一步的设计，实际上是为了让模型有一个明确的起点和终点，避免在复杂分布中迷失方向。
反向扩散过程：从噪声中“重建”数据的本质
反向过程要从完全随机的噪声中逐步还原出原始数据，这一步是整个Diffusion Model的核心，它通过训练神经网络，学习如何在每一步中去除噪声，最终将噪声还原为有意义的数据样本。反向过程并不是简单地“撤销”正向过程，而是通过学习噪声的逆操作，逐步还原数据的本质特征。每一步的去噪操作都相当于在问：“如果我现在有一个带噪声的样本，它最可能的前一步是什么样子？”通过这种方式，模型能够逐步剥离噪声，最终还原出原始数据。这种逐步逼近的方式，不仅让学习任务变得可控，还让模型能够捕捉到数据的深层结构。
这两个过程的存在，实际上是为了应对生成模型中的一个核心难题：如何在复杂的分布中采样 。生成模型，比如GAN，直接从随机噪声中生成数据，但这种方式容易导致模式崩塌（mode collapse），即生成的样本多样性不足。而Denoising Diffusion Model通过正向和反向过程，把生成任务分解成多个小步骤，每一步都只学习一个简单的任务——添加或去除噪声。这种分步学习的方式，不仅提高了模型的稳定性，还显著提升了生成样本的质量和多样性。
正向扩散过程
我们令x 0 \mathbf{x_0} x 0 q ( x ) \mathbb{q(x)} q ( x ) 0 0 0 T T T x T \mathbf{x_T} x T x T ∼ N ( 0 , I ) \mathbf{x_T} \sim \mathcal{N}(\mathbf{0},\mathbf{I}) x T ∼ N ( 0 , I ) 2
正向扩散过程定义为马尔科夫过程（即当前步t t t t − 1 t-1 t − 1
q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) \begin{equation}
q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) = \prod^T_{t=1} q(\mathbf{x}_t \vert \mathbf{x}_{t-1})
\end{equation} q ( x 1 : T ∣ x 0 ) = t = 1 ∏ T q ( x t ∣ x t − 1 ) 其中每一步加的噪音q ( x t ∣ x t − 1 ) q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) q ( x t ∣ x t − 1 )
q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) \begin{equation}
q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I})
\end{equation} q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) 利用重参数化(Reparameterization Trick)从N ( x t ; 1 − β t x t − 1 , β t I ) \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) N ( x t ; 1 − β t x t − 1 , β t I )
x t = 1 − β t x t − 1 + β t ϵ t , ϵ t ∼ N ( 0 , I ) \begin{equation}
\mathbf{x_t} = \sqrt{1-\beta_t}\mathbf{x_{t-1}} + \sqrt{\beta_t}\epsilon_{t}, \quad \epsilon_t \sim \mathcal{N}(\mathbf{0},\mathbf{I})
\end{equation} x t = 1 − β t x t − 1 + β t ϵ t , ϵ t ∼ N ( 0 , I ) tip
正态分布的线性变换性质：可以将标准正态分布转换为任意均值和方差的正态分布 若随机变量Z ∼ N ( 0 , 1 ) Z\sim \mathcal{N}(0,1) Z ∼ N ( 0 , 1 ) μ \mu μ σ \sigma σ X = μ + σ Z X=\mu + \sigma Z X = μ + σ Z X ∼ N ( μ , σ 2 ) X \sim \mathcal{N}(\mu, \sigma^2) X ∼ N ( μ , σ 2 )
重参数化(Reparameterization Trick)技巧是一种将随机变量的采样过程分解为确定性部分和随机噪声部分的方法
X = μ ⏟ 确定性参数 + σ ϵ ⏟ 随机噪声 , ϵ ∼ N ( 0 , 1 ) X = \underbrace{\mu}_{确定性参数} + \sigma \underbrace{\epsilon}_{随机噪声}, \quad \epsilon \sim \mathcal{N}(0,1) X = 确定性参数 μ + σ 随机噪声 ϵ , ϵ ∼ N ( 0 , 1 ) 重参数化计算得到的随机变量x t x_t x t N ( μ , σ 2 ) \mathcal{N}(\mu, \sigma^2) N ( μ , σ 2 )
Parameterization of β t \beta_t β t
β t \beta_t β t
β t \beta_t β t 2 β t \beta_t β t β 1 = 10 − 4 \beta_1=10^{-4} β 1 = 1 0 − 4 β T = 0.02 \beta_T=0.02 β T = 0.02 T = 1000 T=1000 T = 1000 [ − 1 , 1 ] [-1,1] [ − 1 , 1 ] β t \beta_t β t
为什么使用β t \sqrt{\beta_t} β t
这会涉及到两种不同的控制方差的方法：Variance Exploding vs Variance Preserving。
x t = x t − 1 + β t ϵ x_t=x_{t-1} + \sqrt \beta_t \epsilon x t = x t − 1 + β t ϵ 假设初始方差是V a r ( x 0 ) = I Var(x_0)=I Va r ( x 0 ) = I V a r ( x 1 ) = V a r ( x 0 ) + β 1 I = I + β 1 I Var(x_1)=Var(x_0)+\beta_1 I=I+\beta_1 I Va r ( x 1 ) = Va r ( x 0 ) + β 1 I = I + β 1 I V a r ( x T ) = V a r ( x 0 ) + ∑ t = 1 T β t Var(x_T)=Var(x_0)+\sum_{t=1}^{T}\beta_t Va r ( x T ) = Va r ( x 0 ) + ∑ t = 1 T β t T T T I + ∑ t = 1 T β t I+\sum_{t=1}^{T}\beta_t I + ∑ t = 1 T β t T T T
Variance Preserving方差保持
DDPM采用的是这个控制方差的方法通过缩放避免方差爆炸：
x t = α t x t − 1 + β t ϵ , α t + β t = 1 x_t=\sqrt \alpha_t x_{t-1} + \sqrt \beta_t \epsilon, \quad \alpha_t + \beta_t=1 x t = α t x t − 1 + β t ϵ , α t + β t = 1 方差的变化：V a r ( x 1 ) = α 1 V a r ( x 0 ) + β 1 I = I Var(x_1)=\alpha_1 Var(x_0) + \beta_1 I = I Va r ( x 1 ) = α 1 Va r ( x 0 ) + β 1 I = I V a r ( x T ) Var(x_T) Va r ( x T )
重写采样公式
我们试着展开上面的采样公式，展开之前，我们先对变量做一些变换，有助于公式的推导，令α t = 1 − β t \alpha_t=1-\beta_t α t = 1 − β t
x t = α t x t − 1 + 1 − α t ϵ t = α t ( α t − 1 x t − 2 + 1 − α t − 1 ϵ t − 1 ) + 1 − α t ϵ t = α t α t − 1 x t − 2 + α t ( 1 − α t − 1 ) ϵ t − 1 + 1 − α t ϵ t ⏟ i.i.d gaussian noise \begin{align}
\mathbf{x_t} &= \sqrt{\alpha_t}\mathbf{x_{t-1}} + \sqrt{1-\alpha_t}\epsilon_{t} \\
&=\sqrt{\alpha_t}( \sqrt{\alpha_{t-1}}\mathbf{x_{t-2}} + \sqrt{1-\alpha_{t-1}}\epsilon_{t-1}) + \sqrt{1-\alpha_t}\epsilon_{t} \\
&=\sqrt{\alpha_t\alpha_{t-1}}\mathbf{x_{t-2}} + \underbrace{ \sqrt{\alpha_t(1-\alpha_{t-1})}\epsilon_{t-1} + \sqrt{1-\alpha_t}\epsilon_{t}}_{\text{i.i.d gaussian noise}}
\end{align} x t = α t x t − 1 + 1 − α t ϵ t = α t ( α t − 1 x t − 2 + 1 − α t − 1 ϵ t − 1 ) + 1 − α t ϵ t = α t α t − 1 x t − 2 + i.i.d gaussian noise α t ( 1 − α t − 1 ) ϵ t − 1 + 1 − α t ϵ t 如果继续展开更多步，噪声项会变得越来越多，因为都是独立同分布的噪声项，由于正态分布是可以叠加的，可以对噪声项进行简化。注意到α t ( 1 − α t − 1 ) ϵ t − 1 ∼ N ( 0 , α t ( 1 − α t − 1 ) I ) \sqrt{\alpha_t(1-\alpha_{t-1})}\epsilon_{t-1} \sim \mathcal{N}(0,\alpha_t(1-\alpha_{t-1})\mathbf{I}) α t ( 1 − α t − 1 ) ϵ t − 1 ∼ N ( 0 , α t ( 1 − α t − 1 ) I ) ϵ t − 1 ∼ N ( 0 , I ) \epsilon_{t-1} \sim \mathcal{N}(\mathbf{0},\mathbf{I}) ϵ t − 1 ∼ N ( 0 , I ) 1 − α t ϵ t ∼ N ( 0 , ( 1 − α t ) I ) \sqrt{1-\alpha_t}\epsilon_{t} \sim \mathcal{N}(0,(1-\alpha_{t})\mathbf{I}) 1 − α t ϵ t ∼ N ( 0 , ( 1 − α t ) I ) N ( 0 , α t ( 1 − α t − 1 ) + ( 1 − α t ) I ) = N ( 0 , ( 1 − α t α t − 1 ) I ) \mathcal{N}(0,\alpha_t(1-\alpha_{t-1})+(1-\alpha_{t})\mathbf{I})=\mathcal{N}(\mathbf{0}, (1-\alpha_t\alpha_{t-1})\mathbf{I}) N ( 0 , α t ( 1 − α t − 1 ) + ( 1 − α t ) I ) = N ( 0 , ( 1 − α t α t − 1 ) I ) ϵ ˉ t − 2 \bar{\epsilon}_{t-2} ϵ ˉ t − 2 N ( 0 , I ) \mathcal{N}(\mathbf{0},\mathbf{I}) N ( 0 , I )
α t ( 1 − α t − 1 ) ϵ t − 1 + 1 − α t ϵ t = 1 − α t α t − 1 ϵ ˉ t − 2 \begin{equation}
\sqrt{\alpha_t(1-\alpha_{t-1})}\epsilon_{t-1} + \sqrt{1-\alpha_t}\epsilon_{t}=\sqrt{1-\alpha_t\alpha_{t-1}}\bar{\epsilon}_{t-2}
\end{equation} α t ( 1 − α t − 1 ) ϵ t − 1 + 1 − α t ϵ t = 1 − α t α t − 1 ϵ ˉ t − 2 则，
x t = α t x t − 1 + 1 − α t ϵ t = α t α t − 1 x t − 2 + 1 − α t α t − 1 ϵ ˉ t − 2 \begin{align}
\mathbf{x_t} &= \sqrt{\alpha_t}\mathbf{x_{t-1}} + \sqrt{1-\alpha_t}\epsilon_{t} \\
&= \sqrt{\alpha_t\alpha_{t-1}}\mathbf{x_{t-2}} + \sqrt{1-\alpha_t\alpha_{t-1}}\bar{\epsilon}_{t-2}
\end{align} x t = α t x t − 1 + 1 − α t ϵ t = α t α t − 1 x t − 2 + 1 − α t α t − 1 ϵ ˉ t − 2 我们可以一路推导到x 0 \mathbf{x_0} x 0
x t = α ˉ t x 0 + 1 − α ˉ t ϵ , α ˉ t = ∏ s = 1 t α s \begin{align}
\mathbf{x}_t
&= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}, \quad \bar{\alpha}_t=\prod^t_{s=1}\alpha_s
\end{align} x t = α ˉ t x 0 + 1 − α ˉ t ϵ , α ˉ t = s = 1 ∏ t α s 这个递推公式等价于从下面的分布进行采样：
q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) q(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) 然后，我们再换回来β t = 1 − α t \beta_t=1-\alpha_t β t = 1 − α t
q ( x t ∣ x 0 ) = N ( x t ; 1 − β ˉ t x 0 , β ˉ t I ) q(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{1-\bar{\beta}_t} \mathbf{x}_0, \bar{\beta}_t\mathbf{I}) q ( x t ∣ x 0 ) = N ( x t ; 1 − β ˉ t x 0 , β ˉ t I ) tip
为什么经过T \mathbf{T} T x T \mathbf{x_T} x T
使用中心极限定理可以比较简单的说明。中心极限定理（central limit theorem/CLT）是概率论核心定理之一。假设有独立同分布(i.i.d)的随机变量X 1 , X 2 , . . . , X n \mathbf{X_1, X_2,...,X_n} X 1 , X 2 , ... , X n μ \mu μ σ 2 \sigma^2 σ 2 n n n X ˉ = 1 n ∑ i = 1 n X i \bar{\mathbf{X}}=\frac{1}{n}\sum_{i=1}^{n}\mathbf{X_i} X ˉ = n 1 ∑ i = 1 n X i
X ˉ − μ σ / n ∼ N ( 0 , I ) \frac{\bar{\mathbf{X}}-\mu}{\sigma / \sqrt{n}}
\sim
\mathcal{N}(\mathbf{0},\mathbf{I}) σ / n X ˉ − μ ∼ N ( 0 , I ) 正向扩散过程每一步添加的随机变量都是独立同分布与标准正态分布，因此，最后加和得到的x T x_T x T
逆向扩散过程
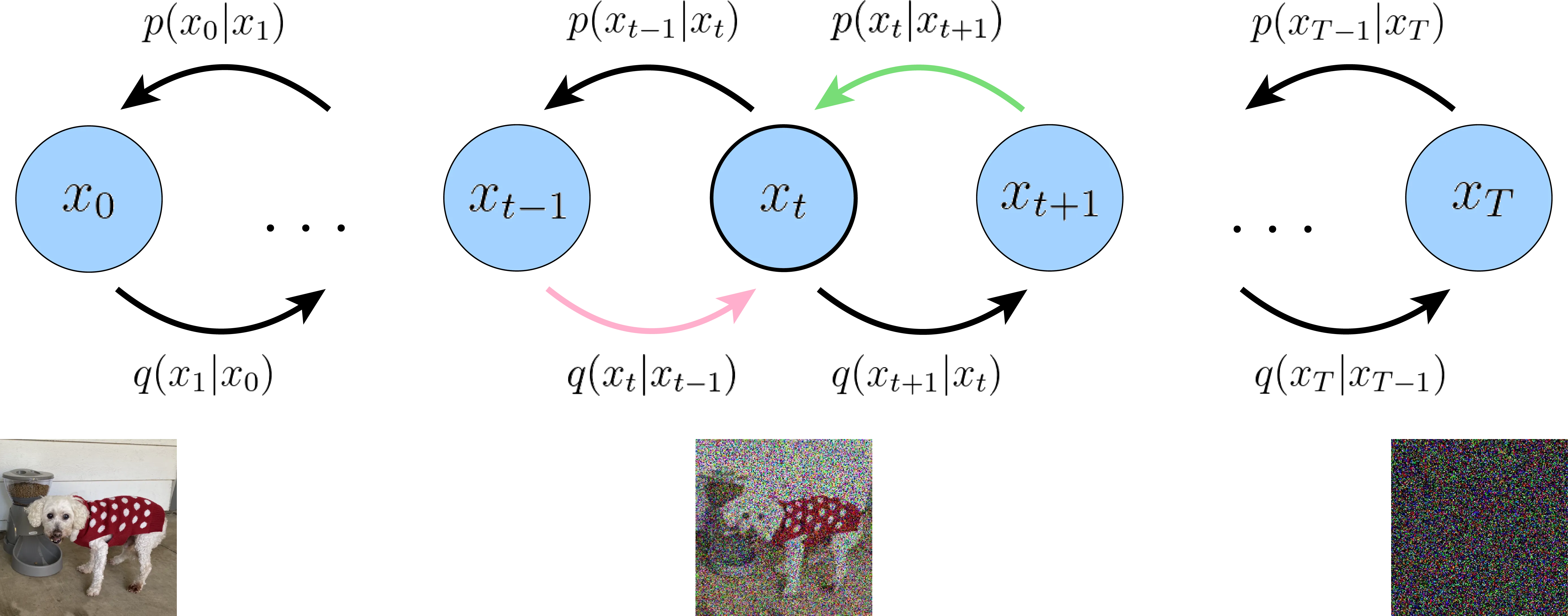
注意这一节中的大量公式可能会比较绕: 正向过程q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) = \prod^T_{t=1} q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) q ( x t − 1 ∣ x t ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) q ( x t − 1 ∣ x t ) p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) \mathbf{p}(\mathbf{x}_T)\prod_{t=1}^{T}\mathbf{p}_{\theta}(\mathbf{x}_{t-1} \vert \mathbf{x}_t) p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t )
逆向扩散过程，即生成过程 ，逐步从噪音(标准正态分布)x T \mathbf{x}_T x T x 0 \mathbf{x}_{0} x 0 q ( x t ∣ x t − 1 ) q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) q ( x t ∣ x t − 1 ) N ( x t ; 1 − β t x t − 1 , β t I ) \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) N ( x t ; 1 − β t x t − 1 , β t I ) q ( x t − 1 ∣ x t ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) q ( x t − 1 ∣ x t ) β t \beta_t β t q ( x t − 1 ∣ x t ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) q ( x t − 1 ∣ x t ) p θ ( x t − 1 ∣ x t ) \mathbf{p}_{\theta}(\mathbf{x}_{t-1} \vert \mathbf{x}_t) p θ ( x t − 1 ∣ x t )
逆向扩散过程同样使用马尔可夫过程来描述：
p θ ( x 0 : T ) = p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) \begin{equation}
\mathbf{p}_{\theta}(\mathbf{x}_{0:T})=\mathbf{p}(\mathbf{x}_T)\prod_{t=1}^{T}\mathbf{p}_{\theta}(\mathbf{x}_{t-1}|\mathbf{x}_t)
\end{equation} p θ ( x 0 : T ) = p ( x T ) t = 1 ∏ T p θ ( x t − 1 ∣ x t ) 其中，θ \theta θ
由于真实的逆向扩散q ( x t − 1 ∣ x t ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) q ( x t − 1 ∣ x t ) 可以假设模型近似的逆向扩散p θ ( x t − 1 ∣ x t ) p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) p θ ( x t − 1 ∣ x t ) ：
p θ ( x t − 1 ∣ x t ) ∼ N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t ) ) p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \sim \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) p θ ( x t − 1 ∣ x t ) ∼ N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t ))
[TODO] 为什么：如果正向过程q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}) q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) β t \beta_t β t q ( x t − 1 ∣ x t ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) q ( x t − 1 ∣ x t ) q ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ ~ ( x t ) , β ~ t I ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\boldsymbol{\mu}}(\mathbf{x}_t), \tilde{\beta}_t \mathbf{I}) q ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ ~ ( x t ) , β ~ t I )
note
多变量联合概率拆分：P ( A , B , C ) = P ( A ∣ B , C ) P ( B ∣ C ) P ( C ) P(A,B,C)=P(A|B,C)P(B|C)P(C) P ( A , B , C ) = P ( A ∣ B , C ) P ( B ∣ C ) P ( C )
由于逆向扩散过程也是马尔科夫过程，所以p ( x 1 , x 2 , … , x T ) = p ( x 1 ∣ x 2 , … , x T ) ⋯ = p ( x 1 ∣ x 2 ) ⋯ p(x_1, x_2, \dots, x_T)=p(x_1|x_2, \dots, x_T)\cdots=p(x_1|x_2)\cdots p ( x 1 , x 2 , … , x T ) = p ( x 1 ∣ x 2 , … , x T ) ⋯ = p ( x 1 ∣ x 2 ) ⋯ x 1 x_1 x 1 x 2 x_2 x 2
优化目标
Diffusion模型优化目标的结论是比较简单的，但是公式的推导和理解是需要静下心来慢慢看懂、推导的！
Variational Lower Bound
与VAE 试图一步生成图像不同，逆向过程逐步去除噪音，可以更好的近似真实的数据分布p ( x 0 ) \mathbf{p(x_0)} p ( x 0 ) 马尔科夫分层自编码器(Markovian Hierarchical Variational Autoencoder,MHVAE) ，此时逆向过程中的x 1 , x 2 , … , x T − 1 \mathbf{x_1, x_2, \dots, x_{T-1}} x 1 , x 2 , … , x T − 1
生成模型的最终目标都是学习到真实数据的分布，即p ( x 0 ) \mathbf{p(x_0)} p ( x 0 ) ，从而可以从其中采样生成非常真实的图像。由于无法对真实数据的分布进行建模，VAE中引入了隐变量z z z p ( x ) = ∫ z p ( x , z ) d z \mathbf{p}(x) = \int_z \mathbf{p}(x,z) dz p ( x ) = ∫ z p ( x , z ) d z log p ( x ) \log p(x) log p ( x ) VAE 博文中):
log p ( x 0 ) = log ∫ x 1 ∫ x 2 ⋯ ∫ x T p ( x 0 , x 1 , … , x T ) d x 1 d x 2 ⋯ d x T = log ∫ x 1 : T p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) d x 1 : T = log ∫ x 1 : T p θ ( x 0 : T ) d x 1 : T q ( x 1 : T ∣ x 0 ) q ( x 1 : T ∣ x 0 ) 引入正向扩散过程 = log ∫ x 1 : T q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) d x 1 : T = log E q ( x 1 : T ∣ x 0 ) [ p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] 期望的定义 ≥ E q ( x 1 : T ∣ x 0 ) log [ p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] : = L V L B via Jensen’s inequality \begin{align}
\log\mathbf{p(x_0)} &= \log \int_{x_1} \int_{x_2} \cdots \int_{x_T} p(x_0, x_1, \dots, x_T) dx_1 dx_2 \cdots dx_T \\
&=\log\int_{x_{1:T}} p(x_T)\prod_{t=1}^{T}p_{\theta}(x_{t-1}|x_t) d_{x_{1:T}} \\
&=\log\int_{x_{1:T}}p_{\theta}(x_{0:T}) d_{x_{1:T}}\frac{q(x_{1:T}|x_0)}{q(x_{1:T}|x_0)} & \small{\text{引入正向扩散过程}} \\
&=\log\int_{x_{1:T}} q(x_{1:T}|x_0)\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}d_{x_{1:T}} \\
&=\log\mathbb{E}_{q(x_{1:T}|x_0)}\Big[\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}\Big] & \small{\text{期望的定义}}\\
&\geq \mathbb{E}_{q(x_{1:T}|x_0)} \log\Big[\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}|x_0)}\Big]:= L_{VLB} & \small{\text{via Jensen's inequality}}
\end{align} log p ( x 0 ) = log ∫ x 1 ∫ x 2 ⋯ ∫ x T p ( x 0 , x 1 , … , x T ) d x 1 d x 2 ⋯ d x T = log ∫ x 1 : T p ( x T ) t = 1 ∏ T p θ ( x t − 1 ∣ x t ) d x 1 : T = log ∫ x 1 : T p θ ( x 0 : T ) d x 1 : T q ( x 1 : T ∣ x 0 ) q ( x 1 : T ∣ x 0 ) = log ∫ x 1 : T q ( x 1 : T ∣ x 0 ) q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) d x 1 : T = log E q ( x 1 : T ∣ x 0 ) [ q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) ] ≥ E q ( x 1 : T ∣ x 0 ) log [ q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) ] := L V L B 引入正向扩散过程 期望的定义 via Jensen’s inequality 优化目标L L L L V L B L_{VLB} L V L B − L V L B -L_{VLB} − L V L B L V L B L_{VLB} L V L B 2
L = − L V L B = − E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] ⏟ L 0 : reconstruction term + E q ( x T − 1 ∣ x 0 ) [ D K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ] ) ⏟ L T : prior matching term + ∑ t = 1 T − 1 E q ( x t − 1 , x t + 1 ∣ x 0 ) [ D K L ( q ( x t ∣ x t − 1 ) ) ∥ p θ ( x t ∣ x t + 1 ] ) ⏟ L T − 1 : consistency term \begin{align}
L &= -L_{VLB} \\
&= \begin{aligned}
&-{\underbrace{\mathbb{E}_{q(x_{1} \vert x_0)}\left[\log p_{\theta}(x_0|x_1)\right]}_{L_{0}\text{: reconstruction term}}}\\
&+ {\underbrace{\mathbb{E}_{q(x_{T-1} \vert x_0)}\left[ D_{KL}(q(x_T \vert x_{T-1}) \parallel {p(x_T)}\right])}_{L_T\text{: prior matching term}}} \\
&+ {\sum_{t=1}^{T-1}\underbrace{\mathbb{E}_{q(x_{t-1}, x_{t+1} \vert x_0)}\left[ D_{KL} (q(x_{t} \vert x_{t-1})) \parallel {p_{\theta}(x_{t}|x_{t+1}}\right])}_{L_{T-1}\text{: consistency term}}}
\end{aligned}
\end{align} L = − L V L B = − L 0 : reconstruction term E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] + L T : prior matching term E q ( x T − 1 ∣ x 0 ) [ D K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ] ) + t = 1 ∑ T − 1 L T − 1 : consistency term E q ( x t − 1 , x t + 1 ∣ x 0 ) [ D K L ( q ( x t ∣ x t − 1 )) ∥ p θ ( x t ∣ x t + 1 ] )
[TODO]详细推导过程:
L = a \begin{aligned}
L &= a
\end{aligned} L = a
请注意的是：上面的公式和DDPM论文公式(5)和What are Diffusion Models?3
注意到优化目标被拆分为三大类，T + 1 T+1 T + 1
DDPM论文中的L 0 L_0 L 0 x 1 x_1 x 1 x 0 x_0 x 0 L 0 L_0 L 0 3.3 3.3 3.3
DDPM论文中的L T L_T L T p ( x T ) p(x_T) p ( x T ) q ( x T ∣ x T − 1 ) q(x_T \vert x_{T-1}) q ( x T ∣ x T − 1 )
DDPM论文中的L T − 1 L_{T-1} L T − 1 正向 扩散q ( x t ∣ x t − 1 ) q(x_{t}\vert x_{t-1}) q ( x t ∣ x t − 1 ) p θ ( x t ∣ x t + 1 ) p_{\theta}(x_t\vert x_{t+1}) p θ ( x t ∣ x t + 1 ) x t x_t x t x t x_t x t x t − 1 , x t + 1 x_{t-1}, x_{t+1} x t − 1 , x t + 1 L T − 1 L_{T-1} L T − 1 4
Rewrite Variational Lower Bound
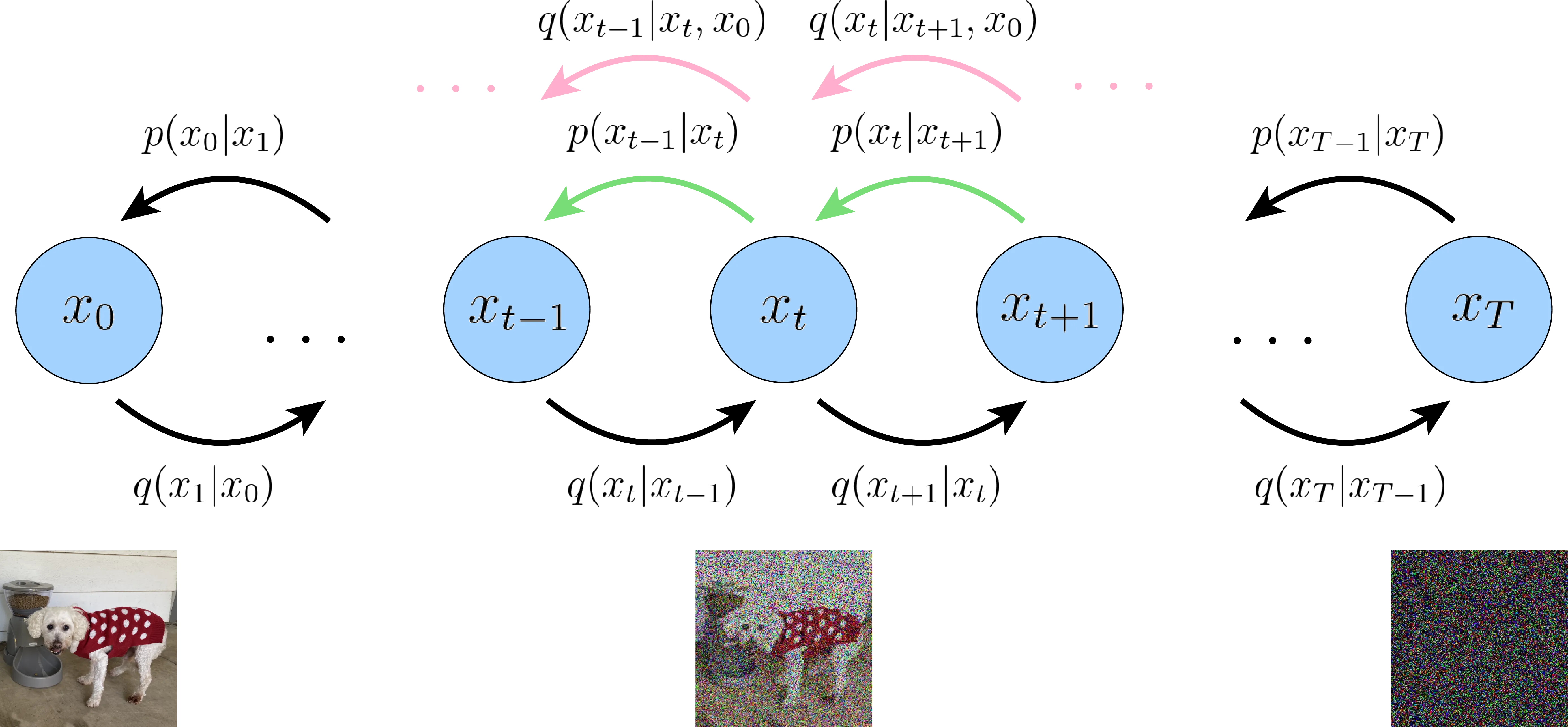
对L T − 1 L_{T-1} L T − 1 q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 ) q(x_t \vert x_{t-1}) = q(x_t \vert x_{t-1}, x_0) q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 ) x 0 x_0 x 0 x 0 x_0 x 0 L L L q ( x t ∣ x t − 1 ) q(x_t \vert x_{t-1}) q ( x t ∣ x t − 1 ) q ( x t ∣ x t − 1 , x 0 ) q(x_t \vert x_{t-1}, x_0) q ( x t ∣ x t − 1 , x 0 )
首先，对L L L
将q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 ) q(x_t \vert x_{t-1}) = q(x_t \vert x_{t-1}, x_0) q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 )
q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) q(x_t \vert x_{t-1}, x_0) = \frac{q(x_{t-1} \vert x_t, x_0)q(x_t \vert x_0)}{q(x_{t-1} \vert x_0)} q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x 0 ) q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) 带入上式到前面的公式( 17 ) (17) ( 17 ) L L L
L = − L V L B = − E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] ⏟ L 0 : reconstruction term + E q ( x T − 1 ∣ x 0 ) [ D K L ( q ( x T ∣ x 0 ) ∥ p ( x T ) ] ) ⏟ L T : prior matching term + ∑ t = 2 T E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ) ∥ p θ ( x t − 1 ∣ x t ] ) ⏟ L T − 1 : denoising matching term \begin{align}
L &= -L_{VLB} \\
&= \begin{aligned}
&-{\underbrace{\mathbb{E}_{q(x_{1} \vert x_0)}\left[\log p_{\theta}(x_0|x_1)\right]}_{L_{0}\text{: reconstruction term}}}\\
&+ {\underbrace{\mathbb{E}_{q(x_{T-1} \vert x_0)}\left[ D_{KL}(q(x_T \vert x_{0}) \parallel {p(x_T)}\right])}_{L_T\text{: prior matching term}}} \\
&+ {\sum_{t=2}^{T}\underbrace{\mathbb{E}_{q(x_{t} \vert x_0)}\left[ D_{KL} (q(\red{x_{t-1} \vert x_{t}, x_0})) \parallel {p_{\theta}(x_{t-1} \vert x_{t}}\right])}_{L_{T-1}\text{: denoising matching term}}}
\end{aligned}
\end{align} L = − L V L B = − L 0 : reconstruction term E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] + L T : prior matching term E q ( x T − 1 ∣ x 0 ) [ D K L ( q ( x T ∣ x 0 ) ∥ p ( x T ) ] ) + t = 2 ∑ T L T − 1 : denoising matching term E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 )) ∥ p θ ( x t − 1 ∣ x t ] )
[TODO]详细推导过程2:
L = a \begin{aligned}
L &= a
\end{aligned} L = a
此时得到的优化目标和DDPM论文终于一致，看下每一项都有什么变化：
重建项L 0 L_0 L 0
先验匹配项L T L_T L T q ( x T ∣ x T − 1 ) q(x_T \vert x_{T-1}) q ( x T ∣ x T − 1 ) q ( x T ∣ x 0 ) q(x_T \vert x_{0}) q ( x T ∣ x 0 )
L T − 1 L_{T-1} L T − 1 正向 扩散q ( x t ∣ x t − 1 ) q(x_{t} \vert x_{t-1}) q ( x t ∣ x t − 1 ) 逆向 扩散q ( x t − 1 ∣ x t , x 0 ) q(\red{x_{t-1} \vert x_{t}, x_0}) q ( x t − 1 ∣ x t , x 0 ) p θ ( x t ∣ x t − 1 ) p_{\theta}(x_t \vert x_{t-1}) p θ ( x t ∣ x t − 1 ) x 0 x_0 x 0 x t x_t x t
现在问题是如何处理q ( x t − 1 ∣ x t , x 0 ) q(\red{x_{t-1} \vert x_{t}, x_0}) q ( x t − 1 ∣ x t , x 0 ) q ( x t − 1 ∣ x t ) q(x_{t-1}\vert x_t) q ( x t − 1 ∣ x t ) x 0 x_0 x 0
第二，可计算的q ( x t ∣ x t − 1 , x 0 ) q(x_t \vert x_{t-1}, x_0) q ( x t ∣ x t − 1 , x 0 )
逆向过程 中提到，q ( x t − 1 ∣ x t ) q(x_{t-1} \vert x_{t}) q ( x t − 1 ∣ x t ) x 0 x_0 x 0 q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; μ ~ ( x t , x 0 ) , β ~ t I ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; {\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0), {\tilde{\beta}_t} \mathbf{I}) q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; μ ~ ( x t , x 0 ) , β ~ t I )
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) via Gaussian PDF ∝ exp ( − 1 2 ( ( x t − α t x t − 1 ) 2 β t + ( x t − 1 − α ˉ t − 1 x 0 ) 2 1 − α ˉ t − 1 − ( x t − α ˉ t x 0 ) 2 1 − α ˉ t ) ) = exp ( − 1 2 ( x t 2 − 2 α t x t x t − 1 + α t x t − 1 2 β t + x t − 1 2 − 2 α ˉ t − 1 x 0 x t − 1 + α ˉ t − 1 x 0 2 1 − α ˉ t − 1 − ( x t − α ˉ t x 0 ) 2 1 − α ˉ t ) ) = exp ( − 1 2 ( ( α t β t + 1 1 − α ˉ t − 1 ) x t − 1 2 − ( 2 α t β t x t + 2 α ˉ t − 1 1 − α ˉ t − 1 x 0 ) x t − 1 + C ( x t , x 0 ) ) ) \begin{aligned}
q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)
&= q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \quad \small{\text{via Gaussian PDF}} \\
&\propto \exp \Big(-\frac{1}{2} \big(\frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\
&= \exp \Big(-\frac{1}{2} \big(\frac{\mathbf{x}_t^2 - 2\sqrt{\alpha_t} \mathbf{x}_t \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \alpha_t} \color{red}{\mathbf{x}_{t-1}^2} }{\beta_t} + \frac{ \color{red}{\mathbf{x}_{t-1}^2} \color{black}{- 2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0} \color{blue}{\mathbf{x}_{t-1}} \color{black}{+ \bar{\alpha}_{t-1} \mathbf{x}_0^2} }{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\
&= \exp\Big( -\frac{1}{2} \big( \color{red}{(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})} \mathbf{x}_{t-1}^2 - \color{blue}{(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)} \mathbf{x}_{t-1} \color{black}{ + C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big)}
\end{aligned} q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) via Gaussian PDF ∝ exp ( − 2 1 ( β t ( x t − α t x t − 1 ) 2 + 1 − α ˉ t − 1 ( x t − 1 − α ˉ t − 1 x 0 ) 2 − 1 − α ˉ t ( x t − α ˉ t x 0 ) 2 ) ) = exp ( − 2 1 ( β t x t 2 − 2 α t x t x t − 1 + α t x t − 1 2 + 1 − α ˉ t − 1 x t − 1 2 − 2 α ˉ t − 1 x 0 x t − 1 + α ˉ t − 1 x 0 2 − 1 − α ˉ t ( x t − α ˉ t x 0 ) 2 ) ) = exp ( − 2 1 ( ( β t α t + 1 − α ˉ t − 1 1 ) x t − 1 2 − ( β t 2 α t x t + 1 − α ˉ t − 1 2 α ˉ t − 1 x 0 ) x t − 1 + C ( x t , x 0 ) ) ) 其中，C ( x t , x 0 ) C(\mathbf{x}_t, \mathbf{x}_0) C ( x t , x 0 ) x t − 1 \mathbf{x}_{t-1} x t − 1 q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; μ ~ ( x t , x 0 ) , β ~ t I ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; {\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0), {\tilde{\beta}_t} \mathbf{I}) q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; μ ~ ( x t , x 0 ) , β ~ t I )
β ~ t = 1 − α ˉ t − 1 1 − α ˉ t β t μ ~ t ( x t , x 0 ) = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t + α ˉ t − 1 β t 1 − α ˉ t x 0 \begin{align}
\tilde{\beta}_t
&= {\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t} \\
\tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0)
&= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\\
\end{align} β ~ t μ ~ t ( x t , x 0 ) = 1 − α ˉ t 1 − α ˉ t − 1 β t = 1 − α ˉ t α t ( 1 − α ˉ t − 1 ) x t + 1 − α ˉ t α ˉ t − 1 β t x 0 其中，α t = 1 − β t \alpha_t = 1 - \beta_t α t = 1 − β t α ˉ t = ∏ i = 1 t α i \bar{\alpha}_t = \prod_{i=1}^t \alpha_i α ˉ t = ∏ i = 1 t α i
从正向扩散过程可知，x 0 = 1 α ˉ t ( x t − 1 − α ˉ t ϵ t ) \mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t) x 0 = α ˉ t 1 ( x t − 1 − α ˉ t ϵ t ) μ ~ t ( x t , x 0 ) \tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0) μ ~ t ( x t , x 0 )
μ ~ t ( x t ) = 1 α t ( x t − 1 − α t 1 − α ˉ t ϵ t ) \begin{align}
\tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t)
&= {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)}
\end{align} μ ~ t ( x t ) = α t 1 ( x t − 1 − α ˉ t 1 − α t ϵ t ) 最后得到：
q ( x t − 1 ∣ x t , x 0 ) ∼ N ( x t − 1 ; 1 α t ( x t − 1 − α t 1 − α ˉ t ϵ t ) , 1 − α ˉ t − 1 1 − α ˉ t β t I ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \sim \mathcal{N}(\mathbf{x}_{t-1};{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)}, {\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t} \mathbf{I}) q ( x t − 1 ∣ x t , x 0 ) ∼ N ( x t − 1 ; α t 1 ( x t − 1 − α ˉ t 1 − α t ϵ t ) , 1 − α ˉ t 1 − α ˉ t − 1 β t I ) Training Loss
铺垫了这么多，让我们回溯一下，优化目标L L L L T − 1 = ∑ t = 2 T E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ) ∥ p θ ( x t − 1 ∣ x t ] ) L_{T-1}=\sum_{t=2}^{T} \mathbb{E}_{q(x_{t} \vert x_0)}\left[ D_{KL} (q(x_{t-1} \vert x_{t}, x_0)) \parallel {p_{\theta}(x_{t-1} \vert x_{t}}\right]) L T − 1 = ∑ t = 2 T E q ( x t ∣ x 0 ) [ D K L ( q ( x t − 1 ∣ x t , x 0 )) ∥ p θ ( x t − 1 ∣ x t ] ) q ( x t − 1 ∣ x t , x 0 ) ∼ N ( x t − 1 ; 1 α t ( x t − 1 − α t 1 − α ˉ t ϵ t ) , 1 − α ˉ t − 1 1 − α ˉ t β t I ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \sim \mathcal{N}(\mathbf{x}_{t-1};{\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)}, {\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t} \mathbf{I}) q ( x t − 1 ∣ x t , x 0 ) ∼ N ( x t − 1 ; α t 1 ( x t − 1 − α ˉ t 1 − α t ϵ t ) , 1 − α ˉ t 1 − α ˉ t − 1 β t I ) 逆向扩散 中定义p θ ( x t − 1 ∣ x t ) ∼ N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t ) ) p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \sim \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) p θ ( x t − 1 ∣ x t ) ∼ N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t )) L T − 1 L_{T-1} L T − 1
tip
两个高斯分布的KL散度计算：
D K L ( N ( x ; μ x , Σ x ) ∥ N ( y ; μ y , Σ y ) ) = 1 2 [ log Σ y Σ x − d + tr ( Σ y − 1 Σ x ) + ( μ y − μ x ) T Σ y − 1 ( μ y − μ x ) ] D_{KL}({\mathcal{N}(x; {\mu}_x,{\Sigma}_x)} \parallel {\mathcal{N}(y; {\mu}_y,{\Sigma}_y)})
=\frac{1}{2}\left[\log\frac{{\Sigma}_y}{{\Sigma}_x} - d + \text{tr}({\Sigma}_y^{-1}{\Sigma}_x)
+ ({\mu}_y-{\mu}_x)^T {\Sigma}_y^{-1} ({\mu}_y-{\mu}_x)\right] D K L ( N ( x ; μ x , Σ x ) ∥ N ( y ; μ y , Σ y ) ) = 2 1 [ log Σ x Σ y − d + tr ( Σ y − 1 Σ x ) + ( μ y − μ x ) T Σ y − 1 ( μ y − μ x ) ] 其中d d d x x x
在代入公式前，DDPM论文对p θ ( x t − 1 ∣ x t ) ∼ N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t ) ) p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \sim \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t)) p θ ( x t − 1 ∣ x t ) ∼ N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t )) Σ θ ( x t , t ) \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) Σ θ ( x t , t ) q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) q ( x t − 1 ∣ x t , x 0 )
D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) = D K L ( N ( x t − 1 ; μ q , Σ q ( t ) ) ∥ N ( x t − 1 ; μ θ , Σ q ( t ) ) ) = 1 2 [ log Σ q ( t ) Σ q ( t ) − d + tr ( Σ q ( t ) − 1 Σ q ( t ) ) + ( μ θ − μ q ) T Σ q ( t ) − 1 ( μ θ − μ q ) ] = 1 2 [ log 1 − d + d + ( μ θ − μ q ) T Σ q ( t ) − 1 ( μ θ − μ q ) ] = 1 2 [ ( μ θ − μ q ) T Σ q ( t ) − 1 ( μ θ − μ q ) ] = 1 2 [ ( μ θ − μ q ) T ( σ q 2 ( t ) I ) − 1 ( μ θ − μ q ) ] = 1 2 σ q 2 ( t ) [ ∥ μ θ ( x t , t ) − μ q ( x t , x 0 ) ∥ 2 2 ] \begin{aligned}
& \quad \ D_{KL}({q(x_{t-1}|x_t, x_0)} \parallel {p_{{\theta}}(x_{t-1}|x_t)}) \\
&= D_{KL}({\mathcal{N}(x_{t-1}; {\mu}_q,{\Sigma}_q(t))}\parallel{\mathcal{N}(x_{t-1}; {\mu}_{{\theta}},{\Sigma}_q(t))})\\
&=\frac{1}{2}\left[\log\frac{{\Sigma}_q(t)}{{\Sigma}_q(t)} - d + \text{tr}({\Sigma}_q(t)^{-1}{\Sigma}_q(t))
+ ({\mu}_{{\theta}}-{\mu}_q)^T {\Sigma}_q(t)^{-1} ({\mu}_{{\theta}}-{\mu}_q)\right]\\
&=\frac{1}{2}\left[\log1 - d + d + ({\mu}_{{\theta}}-{\mu}_q)^T {\Sigma}_q(t)^{-1} ({\mu}_{{\theta}}-{\mu}_q)\right]\\
&=\frac{1}{2}\left[({\mu}_{{\theta}}-{\mu}_q)^T {\Sigma}_q(t)^{-1} ({\mu}_{{\theta}}-{\mu}_q)\right]\\
&=\frac{1}{2}\left[({\mu}_{{\theta}}-{\mu}_q)^T \left(\sigma_q^2(t)\textbf{I}\right)^{-1} ({\mu}_{{\theta}}-{\mu}_q)\right]\\
&=\frac{1}{2\sigma_q^2(t)}\left[\left\lVert{\mu}_{{\theta}}(\mathbf{x}_t,t)-{\mu}_q(\mathbf{x}_t,\mathbf{x}_0)\right\rVert_2^2\right]
\end{aligned} D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) = D K L ( N ( x t − 1 ; μ q , Σ q ( t )) ∥ N ( x t − 1 ; μ θ , Σ q ( t )) ) = 2 1 [ log Σ q ( t ) Σ q ( t ) − d + tr ( Σ q ( t ) − 1 Σ q ( t )) + ( μ θ − μ q ) T Σ q ( t ) − 1 ( μ θ − μ q ) ] = 2 1 [ log 1 − d + d + ( μ θ − μ q ) T Σ q ( t ) − 1 ( μ θ − μ q ) ] = 2 1 [ ( μ θ − μ q ) T Σ q ( t ) − 1 ( μ θ − μ q ) ] = 2 1 [ ( μ θ − μ q ) T ( σ q 2 ( t ) I ) − 1 ( μ θ − μ q ) ] = 2 σ q 2 ( t ) 1 [ ∥ μ θ ( x t , t ) − μ q ( x t , x 0 ) ∥ 2 2 ] 到这里可以发现，最终模型的优化目标是q ( x t − 1 ∣ x t , x 0 ) q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) q ( x t − 1 ∣ x t , x 0 ) μ q ( x t , x 0 ) {\mu}_q(\mathbf{x}_t,\mathbf{x}_0) μ q ( x t , x 0 ) μ θ ( x t , t ) \mu_{\theta}(\mathbf{x}_t,t) μ θ ( x t , t ) μ q ( x t , x 0 ) {\mu}_q(\mathbf{x}_t,\mathbf{x}_0) μ q ( x t , x 0 ) μ θ ( x t , t ) \mu_{\theta}(\mathbf{x}_t,t) μ θ ( x t , t ) ( 24 ) (24) ( 24 ) DDPM2 1 ϵ t \epsilon_t ϵ t x t x_t x t t t t ϵ θ ( x t , t ) {\epsilon}_{ {\theta}}(x_t, t) ϵ θ ( x t , t ) ：
μ θ ( x t , t ) = 1 α t x t − 1 − α t 1 − α ˉ t α t ϵ θ ( x t , t ) {\mu}_{{\theta}}(x_t, t) = \frac{1}{\sqrt{\alpha_t}}x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar\alpha_t}\sqrt{\alpha_t}} {\epsilon}_{ {\theta}}(x_t, t) μ θ ( x t , t ) = α t 1 x t − 1 − α ˉ t α t 1 − α t ϵ θ ( x t , t ) 近似函数ϵ θ ( x t , t ) \epsilon_{\theta}(x_t, t) ϵ θ ( x t , t ) x t x_t x t ϵ \epsilon ϵ
1 2 σ q 2 ( t ) [ ∥ μ θ ( x t , t ) − μ ~ t ( x t , x 0 ) ∥ 2 ] = 1 2 σ q 2 ( t ) [ ∥ 1 α t ( x t − 1 − α t 1 − α ˉ t ϵ θ ( x t , t ) ) − 1 α t ( x t − 1 − α t 1 − α ˉ t ϵ t ) ∥ 2 ] = ( 1 − α t ) 2 2 α t ( 1 − α ˉ t ) σ q 2 ( t ) [ ∥ ϵ θ ( x t , t ) − ϵ t ∥ 2 ] = ( 1 − α t ) 2 2 α t ( 1 − α ˉ t ) σ q 2 ( t ) [ ∥ ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ t , t ) − ϵ t ∥ 2 ] \begin{aligned}
& \quad \frac{1}{2\sigma_q^2(t)}\Big[ \| {{\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)- \tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)}} \|^2 \Big] \\
&= \frac{1}{2\sigma_q^2(t)} \Big[ \| {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) \Big)} - {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} \|^2 \Big] \\
&= \frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \sigma_q^2(t)} \Big[ \|\boldsymbol{\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) - \epsilon}_t \|^2 \Big] \\
&= \frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \sigma_q^2(t)} \Big[\|\boldsymbol{\boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)-\epsilon}_t\|^2 \Big]
\end{aligned} 2 σ q 2 ( t ) 1 [ ∥ μ θ ( x t , t ) − μ ~ t ( x t , x 0 ) ∥ 2 ] = 2 σ q 2 ( t ) 1 [ ∥ α t 1 ( x t − 1 − α ˉ t 1 − α t ϵ θ ( x t , t ) ) − α t 1 ( x t − 1 − α ˉ t 1 − α t ϵ t ) ∥ 2 ] = 2 α t ( 1 − α ˉ t ) σ q 2 ( t ) ( 1 − α t ) 2 [ ∥ ϵ θ ( x t , t ) − ϵ t ∥ 2 ] = 2 α t ( 1 − α ˉ t ) σ q 2 ( t ) ( 1 − α t ) 2 [ ∥ ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ t , t ) − ϵ t ∥ 2 ] 其中ϵ t \epsilon_t ϵ t t − 1 t-1 t − 1 t t t 模型从预测均值μ t \mu_t μ t ϵ t \epsilon_t ϵ t 。
Simplified Loss
DDPM论文中，通过实验发现，忽略上面公式中的权重( 1 − α t ) 2 2 α t ( 1 − α ˉ t ) σ q 2 ( t ) \frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t)\sigma_q^2(t)} 2 α t ( 1 − α ˉ t ) σ q 2 ( t ) ( 1 − α t ) 2
L t simple = E t ∼ [ 1 , T ] , x 0 , ϵ t [ ∥ ϵ θ ( x t , t ) − ϵ t ∥ 2 ] = E t ∼ [ 1 , T ] , x 0 , ϵ t [ ∥ ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ t , t ) ∥ 2 − ϵ t ] \begin{aligned}
L_t^\text{simple}
&= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\| \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) - \boldsymbol{\epsilon}_t \|^2 \Big] \\
&= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 - \boldsymbol{\epsilon}_t \Big]
\end{aligned} L t simple = E t ∼ [ 1 , T ] , x 0 , ϵ t [ ∥ ϵ θ ( x t , t ) − ϵ t ∥ 2 ] = E t ∼ [ 1 , T ] , x 0 , ϵ t [ ∥ ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ t , t ) ∥ 2 − ϵ t ] Training and Sampling (Generate)
训练过程见如下伪代码：
从标准高斯分布中随机采样一个噪声，注意每一个时刻都是独立重新采样的随机高斯噪声，所以不同步t t t ϵ \epsilon ϵ
代入上式中计算得到x t x_t x t
把x t x_t x t t t t ϵ θ ( x t , t ) \epsilon_{{\theta}}(x_t, t) ϵ θ ( x t , t )
最小化ϵ \epsilon ϵ ϵ θ ( x t , t ) \epsilon_{{\theta}}(x_t, t) ϵ θ ( x t , t )
采样过程，即生成过程的伪代码如下：
x ~ 0 \tilde{x}_0 x ~ 0 x t − 1 x_{t-1} x t − 1 x 0 x_0 x 0 t = 1 t=1 t = 1 x ~ 0 \tilde{x}_0 x ~ 0 μ ~ \tilde{\mu} μ ~
μ ~ = 1 α t ( x t − β t 1 − α t ˉ ϵ θ ( x t , t ) ) = 1 α 1 ( x 1 − 1 − α 1 1 − α 1 ˉ ϵ ˉ ) = 1 α 1 ( x 1 − 1 − α 1 1 − α 1 ˉ ϵ ˉ ) = 1 α 1 ( x 1 − 1 − α 1 1 − α 1 ϵ ˉ ) = 1 α 1 ( x 1 − 1 − α 1 ϵ ˉ ) = x ~ 0 \begin{align}\begin{aligned}\tilde{\mu} &= \frac{1} {\sqrt{\alpha_t}} (x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha_t}} } \epsilon_{\theta}(x_t,t) )\\&= \frac{1} {\sqrt{\alpha_1}} (x_1 - \frac{1-\alpha_1}{\sqrt{1-\bar{\alpha_1}} } \bar{\epsilon} )\\&= \frac{1} {\sqrt{\alpha_1}} (x_1 - \frac{1-\alpha_1}{\sqrt{1-\bar{\alpha_1}} } \bar{\epsilon} )\\&= \frac{1} {\sqrt{\alpha_1}} (x_1 - \frac{1-\alpha_1}{\sqrt{1-\alpha_1} } \bar{\epsilon} )\\&= \frac{1} {\sqrt{\alpha_1}} (x_1 - \sqrt{1-\alpha_1} \bar{\epsilon} )\\&= \tilde{x}_0\end{aligned}\end{align} μ ~ = α t 1 ( x t − 1 − α t ˉ β t ϵ θ ( x t , t )) = α 1 1 ( x 1 − 1 − α 1 ˉ 1 − α 1 ϵ ˉ ) = α 1 1 ( x 1 − 1 − α 1 ˉ 1 − α 1 ϵ ˉ ) = α 1 1 ( x 1 − 1 − α 1 1 − α 1 ϵ ˉ ) = α 1 1 ( x 1 − 1 − α 1 ϵ ˉ ) = x ~ 0
也就是说我们最终输出的x ~ 0 \tilde{x}_0 x ~ 0 q ( x t − 1 ∣ x t , x 0 , t = 1 ) q(x_{t-1}|x_t, x_0,t=1) q ( x t − 1 ∣ x t , x 0 , t = 1 ) q ( x t − 1 ∣ x t , x 0 , t = 1 ) q(x_{t-1}|x_t, x_0,t=1) q ( x t − 1 ∣ x t , x 0 , t = 1 )
在采样（图像生成）过程有一个细节，最后生成的图像(输出值)并不是通过计算得到的。而最终生成的图像是根据下面公式得到的，当时，和是相等的，